Common Attack Graph Schema (CAGS) 3.2

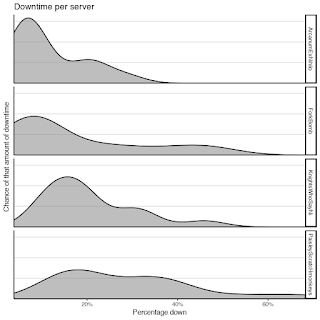
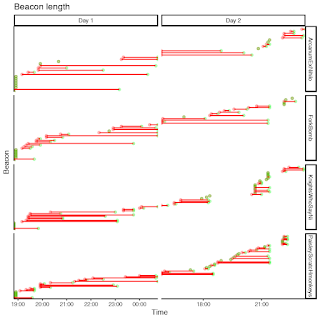
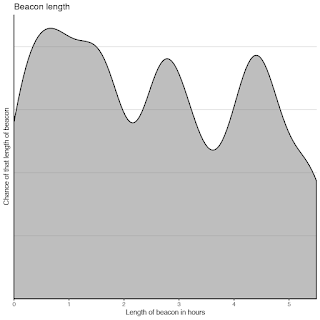
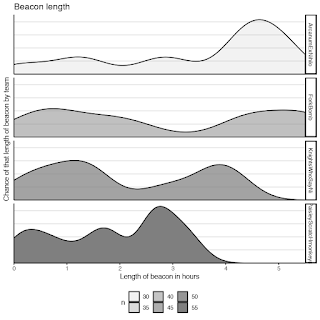
 It's been a while since I've updated CAGS. This is an initial post and may be modified to better fit with CAGS 2 later.

Revision: Schema updated to 3.2.  See the previous 3.X schema(s) at the end of this post.

3.2 Schema

1. All property names must be stored as lower case
2. The graph must be a directed multigraph.  It must be a combination of a causal bipartite multigraph with 'context, 'objects' (previously conditions, a subtype of context), and 'actions' (previously events) representing the two types of nodes and a knowledge simple graph defined in OWL used to describe the objects and actions.
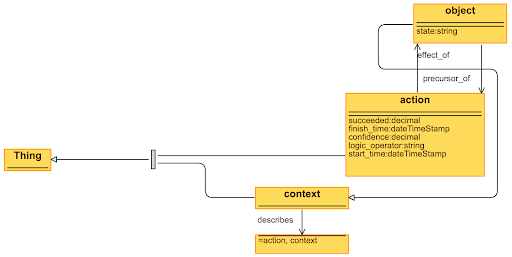
3. Action node properties.  All other properties should be defined through the knowledge graph.
1. type: "action" (required)
2. id: A URI including the graph prefix identifying the node (required)
3. name: The action that occured.  This may be from a schema such as a VERIS action or ATT&CK technique, or may be an arbitrary string describing the action or event that took place. (required)
4. start_time: The time the atomic the node represents began to exist.  Time should be in ISO 8601 combined date and time format (e.g. 2014-11-01T10:34Z).  If no time is available, minutes since unix epoch (1/1/1970 Midnight UTC) should be used as a sequence number. (required)
5. finish_time: The time the atomic the node represents ceased to exist.  Time should be in ISO 8601 combined date and time format (e.g. 2014-11-01T10:34Z) (optional but encouraged)
6. logic_operator: a function (including the language the function is defined in) that takes the state of parent objects to the node as arguments (pre-conditions) and returns the effect(s) on child objects to the node (effects).  (A characteristic borrowed from formal planning.) This may be ladder logic, first order logic, higher level languages such as python, machine learning model, etc. The values accepted per pre-condition and produced per effect must be in the same set as values used for the object node state property. In practice this will often be the identity function.  (For example if a parent object's state is 'compromised', after the action the child object's state will be compromised.  If missing, is assumed to be the identity operator transfering the set of all state from precursor objects to affected objects.
7. succeeded: float from 0 (failed) to 1 (succeeded) or distribution representing the probability that action succeeded in its effects. Any effects which may be separable should be defined through a separate action. (optional)
8. confidence: float from 0 to 1 or distribution representing the confidence that the action succeeded. (optional)
4. Context node properties.  All other properties should be defined through the knowledge graph.  These definitions may take the from of an existing schema such as VERIS assets, the CARS data model objects, or other ontologies of objects defined through a knowledge graph.
1. type: "context" or "object" (required)
2. id: A URI including the graph prefix identifying the node (required)
5. Object node properties.  Object nodes are a sub-type of context in that they may be instanced and have a 'state' which changes as actions are applied.  Only object nodes may be part of the causal graph.
1. state: A property that may be used as a transient string representing the state of the object during a point in time representing the current state of the system.  The sum of all object states is the state of the system.  This may be as simple as "compromised", from an ontology such as VERIS attributes, the Confidentiality, Integrity, Availability triad, Bayesian or DIMFUI (Degradation, Interruption, Modification, Fabrication, Unauthorized Use, and Interception), or it may even be an arbitrary string.
6. Edge Properties:
1. source: the id of the source node. Object nodes may only have sources of action nodes and action nodes may only have sources of object nodes. All nodes part of the knowledge graph may only have sources within the knowledge graph or an object node. (required)
2. destination: the id of the destination node. Object nodes may only have destinations of action nodes and action nodes may only have destinations of object nodes. All nodes part of the knowledge graph may only have sources within the knowledge graph or an object node. (required)
3. type: Edges between actions and objects (in either direction) have a type from the set of states acceptable for the object node state property and must agree with the pre-conditions and effects of the action node involved's logic operator.  All other edges are defined by the OWL knowledge schema. (required)
1. The acceptable edge types are: "precursor_of" (edge from an object to an action), "effect_of" (edge from an action to an object), "describe" (edge from an object or context to an object, context, or action).
4. id: A URI representing the edge. (optional)
7. It is intended that sets of nodes and edges in the graph can be joined to create a subgraph represented by a single node.  The node must still obey all previous schema requirements.

Strengths

This schema builds on the 2.0 and 3.0 schemas in a few fundamental ways:

• The use of knowledge graphs to provide properties simplifies defining arbitrary sets of properties.  This is incredibly important as different users will want to represent different properties at different levels of detail.  In Figure 1, Object 3 is a process linked to it's higher level representations.  However the dotted lines show how Objects 5-8 could be used if the goal was a higher level representation of the incident.

Figure 1 - Knowledge graph used to represent different levels of description.

• The use of a logic operator allows for arbitrary logic in progressing through the graph without creating complex graph structures to try and define the logic.  This effectively replaces the Bayesian Conditional Probability Tables in version 2.
• The action-object bipartite graph provides the ability to represent complex relationships (as a bipartite graph can represent hypergraphs and simplicial complexes, or dendrites) while still maintaining the strengths of traditional graphs.  It allow allows moving almost all properties to nodes or to the knowledge graph.
• The use of properties defined without schemas (action node action, action node logic operator, object node knowledge graph, and object node state) allows the schema to be "specifically vague" (credit to Gage for the term).  Enough to be clear but vague enough to support varying use cases.
• The set of object states is the state of the system the graph describes.  To determine the state of the graph at given time, all actions must be applied in order. This provides for state management without state explosion.

Limitations

• The schema does not define how parent-child relationships are established (though it is logical that children must come after parents and that parents/children are limited by the objects an action requires tas pre-conditions and the objects it may affect.
• The schema does not define how to identify duplicate objects within the graph (where a a single actual object is represented by two object nodes).  When a schema is not used to help avoid duplication, I envision tools that tools will be available to help identify duplicates through their knowledge graph properties.  OWL allows for the same object to exist as different notes in the same knowledge graph.
• The schema does not readily distinguish between ground truth and records used to observe ground truth.  Care must be taken to distinguish these two types of actions and the associated objects.  For example, a record may be an object child of the action that generated it.  Figure 2 provides an example.  The characteristics of the record can be as simple or as detailed as desired though it's prudent to consider the ability of the graph to scale to represent instances of records.

Figure 2 - Representing logs of what  happened

• The schema does not explicitly define actor, however it may be a relationship established in the knowledge graph and is considered a best practice.

Example

The following image provides an example based on an incident from the VERIS Community Database (VCDB), specifically case a2ed36db-0c78-4162-b2cc-dbaa2ca73866. (Note that the example leaves out the majority of the properties for brevity.)

Figure 3 - Example incident

Representations

At its core, the schema is incredibly simple as can be seen below:

This OWL file can be found here.  CAGS graphs conforming to this format should be stored as triples in JSON-LD format.  If converting to a property graph, the graph should be stored in JSON Graph Format (JGF).

Use Cases

Aggregation of Events  

Log data comes in as atomic events.  Given any single event, timestamps only reveal that later events cannot be the parent and earlier events cannot be the child, but the timestamp does not explain _what_ the parent(s) or child/children of an event are.  

 

The graph schema should assist in determining the parent(s) and child/children of an event, (for example by defining that an event occurred due to a file, a credential, or another system and, as such, that object(s) or actions ending in that object(s) must contain the parent.  

Motif Communication

It is often helpful when communicating a plurality of actions to communicate the relationships between those actions.  This really will touch on multiple use-cases, but is centered around motifs as bounded portion of a path or subgraph.  

Attack Surface  

A system can be documented using the graph schema to identify the interconnectivity between components and highlight potential paths of attack.  (Note, while many of the prior use cases are based around events (or signal generated from the system, this is based on the _actual_ state of the system and actual actions rather than the events they generate.)  

Attack Graph Generation  

An attack surface generated using the graph schema can be used to plan potential attacks on the system.  This can be used for automated attack simulation such as cauldera, planning manual penetration testing (such as bloodhound), etc.  This likely results in an attack graph, (a plurality of actions to take).  

Analysis  

Event data should be able to be aggregated into paths and graphs.  This data can then be aggregated across data sources (different tools, sites, organizations, etc) and then queried using graph queries to identify commonalities such as common motifs.

Incident Documentation  

After an incident has occurred,  the incident responders can document the relationship between the observed actions (or events generated by those actions) using the graph schema.  

Detection  

A defender wants to define a detection that contains multiple atomic events and how they are related (such as in grapl).  To do this they need both a motif of the detection and the ability to aggregate events to see if they match the motif.

Simulation  

A defender may wish to simulate attacks containing more than a single event.  To do so they need a motif of events and their relationships and the ability to turn that into atomic actions to take/attempt to take.

Incident Response  

After aggregating events, the data can be analyzed using graph tools, neural networks, or other tools to identify things like missing edges (actions the attackers might have taken but where no event exists to document it), nodes (objects that may be involved in the incident, but are currently not included in the investigation), or clustering (to identify assets currently part of the investigation but are unlikely to have been involved).  

Defense Planning  

Given analysis of an attack surface producing an attack graph, the attack graph can then be analyzed to determine thing such as what events will be generated if exercised, nodes and edges central to the attack that might serve as optimal mitigation points, etc.

Risk Analysis  

Given an attack surface, analyze the graph to identify the overall 'risk' associated with it.  The goal is to provide quantitative feedback on the likelihood and potentially impact of cyber threats given threat intelligence.  

3.1 SCHEMA

The 3.1 schema is the same as the 3.2 schema except for the following changes:

• The CAGS 3.1 'uuid' property has been replaced with an 'id' which uses URIs including graph namespaces instead of UUIDs
• CAGS 3.2 adds allowed edge types
• CAGS 3.2 adds 'context' nodes
• Added representations
• Described logic_operator as optional but with a default representation if missing
• Renamed the 'action' property of actions to 'name'

3.0 SCHEMA

The attack flows are defined with nodes as objects and their individual actions as hyperedges. Nodes maintain their individuals state with respect to security while edges document how state is changed by the edge. Edges also contain the logic to adjudicate complex interactions between inputs.  The attack flow (or graph) in its entirety represents the state of the system (or portion of the system) being described.

NODES TYPES:

• Datum
• Person
• Storage
• Compute
• Memory
• Network
• Other
• Unknown

Nodes have a ‘state’ property representing their current state with respect to the actor.  They indicate the  states (confidentiality/integrity/availability, Create/Read/Update/Delete, or object-specific).

EDGES:

• leads_to

Edges are hyperedges (or, alternately, a bipartite representation of hyper-edges) with with a ‘logic’ property defining the process for translating the inputs into a success at the output.  Another option is to model the edge as a dendrite to represent the input to output logic of the edge.

Edges have a ‘action’ property defining the details of the action. (These may be in ATT&CK, veris, or any an arbitrary language.)

Edges may have a timestamp property to indicate the order in which they occur.  In practice this can be ‘played’ on the graph to update the node states over time.

Can you predict the future? No.

Did you ever wonder why some people succeed and others don't? Why Jeff Bezos is rich? Why a company got breached?  Is it because Jeff Bezos somehow learned what would happen in the future?  Is it because the breached company ignored the obvious future?  No.  No-one can predict the future.  

Let's take an example: Double Pendulums

Just predict where they'll swing.  Really easy right?  You can model the entire pendulum with two nodes and two edges. Simple.

Give it a try:  https://www.myphysicslab.com/pendulum/double-pendulum-en.html.  Hit the pause button in the upper-right, drag the pendulums to the top where they can drop.  Put your finger on the screen where you think they'll be in 5 seconds, hit play, and count to 5.  How did it go? 

Hmmm.  Let’s try it again.  Maybe if you saw it happen first.  Hit pause, drag them back up, put 1 finger where it starts, run to the count of 5, and put another finger (same hand) where it ends.  Now drag the pendulum back up to the first finger, hit play again, and count to 5.  Is the second pendulum anywhere near your second finger?

You can't predict the future

If you were right you were wildly lucky.  Check out 7 pendulums who's only difference is approximately 1/3rd of an ounce.  It's due to chaotic motion.  Even in a system with just two nodes where we know all the variables, it gets unpredictable very quickly.  Now imagine if your system is something like this:

In this image the color code is as follows:

• the upper-left brown is the internet.  
• the five fuchsia nodes to the right are user systems
• the upper green are the DMZ
• the blue-green and dark grey are servers
• orange are management systems
• light pink is infrastructure
• grey is a security system
• light blue at the bottom is a protected enclave.  

That's about two dozen systems. An _extremely_ small IT estate.  And we have little idea what all the variables it may contain.  Compare that to the two pendulum model.  If we can't predict two pendulums what chance do we have with this?

Try to imagine predicting the business climate and how the world will change over the next 20 years.  You need to make choices now that will govern your success then.  Can you (or anyone) do that?

The answer is, of course, no.  Lots of people are making many decisions and some will be right, and some will be wrong. However, for the most part it's not due to the individuals making them.

So what's a person to do?

Give up? Give in? Nah, don’t do that.

In spite of all the uncertainty and the multitude of variables involved, the reality is that most useful systems do not tend to devolve into chaos.  If they did they wouldn't be useful.  Instead, they normally remain in common, steady states. Except for moving from one steady state to another when something changes.

And that's what you should do.  Bet on the average.  The common state.  The place where most things end up.  Don't look at people who succeeded (or failed) spectacularly.  It was spectacular because it wasn't common. They couldn't predict the future and neither can you.  You can bet on the most common outcome though. (As Sir Francis Galton - or Dan Kahneman if you prefer - would call it, Regression to the Mean.)  For security, this means filter email, filter web content, use two- factor authentication, and manage assets.

The other thing you can do is prepare to change along with the situation.  This requires creative people who can devise innovative solutions when there is some new input, as opposed to rather following the usual processes.  This is one of the reasons why quality security operations are essential. Something engineered and built over several years will never cope with a significant shift in information security unless it also shifts.

And in conclusion, don't beat yourself up over it

What happened in the past did not predictably lead to today, for you or anyone else.  And not only does the past not predict the future, but the future doesn’t require the past.  Inverse evolutionary techniques such as Inverse Generative Social Science demonstrate that things could have started completely differently, and we still could arrive right where we are today.  The best you can do is invest in the average and be creative enough to handle the unanticipated.

Simulating Security Strategy

You’ve probably imagined it, right? Lots of little attackers and defenders going at it in a simulated environment while you look on with glee. But instead of spending our cycles on details such as if the attack gets in, let's leave that for the virtual detonation chambers and focus on the bigger picture of attack and defense?

That is exactly what Complex Competition does.  It simulates an organization as a topology and then allows an attacker and a defender to compete on it.  Table 1 provides all the rules:

1. Gameboard is an undirected, connected, graph. Nodes may be controlled by one or both parties.  One node is marked the goal.

2. The defender party starts with control of all nodes except one.

3. The attacker party starts with control of one node only.

4. Parties take turns. They may:

1. Pay A1/D1 cost to observe the control of a node.  
2. Pay A2/D2 cost to establish control of a node. 
3. Pay A3/D3 cost to remove control from a node (only succeeding if they control the node).
4. A4/D4 cost to discovery peers of a node.
5. Pass or Stop at no cost.

5. They may only act on nodes connected to nodes they control. 

6. The attacker party goes first.

7. The target node(s) is assigned values V1-Vn.  When the attacker gains control of the target node X, they receive value Vx and the defender loses value Vx.

8. The game is over when both parties stop playing.  Once a party has stopped playing, they may not start again.

This allows us to test out a lot of things which include the below:

Does randomly attacking in a network pay? 

Answer: No! (Unless the target of the attack is connected to the internet)

What does it cost to defend?

Answer: anywhere from three to five times the number of actions the attacker took.

What attacker strategies work best if there’s no defender?

Answer: Attacking deep into the network, or trying a quick attack and bailing.

What attacker strategies work best if there is a defender?

Answer: Now the quick attack is a clear front runner.

How does an infrastructure compromise change the attack?

Answer: When the infrastructure is compromised, the attacker doesn’t have to dig deep into the network. (Obvious, I know. But here we can show it quantitatively.)

Now the caveats

All that analysis must be taken with a grain of salt.  It’s totally dependent on the costs of the actions (all 1), the value and locations of the targets, the topology, and the attacker strategy.  None of which are meant to be particularly representative in these simulations.  Also, this simulation is relatively basic, but hopefully it strikes a balance between usefulness and simplicity for this first iteration.

Still, there’s a lot of other questions we could try to answer:

• When should the defender stop defending / how much should they spend on defense?
• How else does the location of the attacker affect their cost to reach the target?
• How does the target location affect the attacker's cost to reach it?
• How do different topologies affect the attacker and defender costs?
• How do different costs affect the attacker's chance of reaching the target?
• What is the relationship between topology, attacker strategy, attacker action cost, and target value?

And eventually we could make it more complex:

• Add more information to the nodes to help players choose actions
• Probability of success per edge
• Cost of action per node
• Replace the undirected graph with a directed graph
• Different value for the attacker and defender for achieving the goal.
• Separating the impact cost to the defender from the goal and having them on separate nodes
• Allow the defender to take more than one action per round
• Set per edge success probabilities and costs
• Create action probabilities
• Allow the defender to pay to increase attacker action cost (potentially per edge).
• Allow the defender to pay to decrease the action success probability (potentially per edge).
• Allow the defender to pay to monitor nodes without having to inspect them

Primarily, though, we simply want to get this out there and give everyone a chance to try it out,   and, more than anything, illustrate the clear need to simulate security strategy. (He said the thing!)

Be the CFP review you want to be reviewed by

There are lots of infosec conferences which means lots of CFPs and lots of talks reviewed. I participate in several and figured I would share some of the lessons I've learned.  A caveat: This is highly opinionated.  It's my experience so probably doesn't apply to everyone.  I mostly do small, specialized tracks and conferences so reviewing dozens of talks, not hundreds.

The CFP

Set yourself up for success.  There are probably 5 things you need to ask for in addition to the speaker info.  If you don't ask for them, you'll end up asking later:

1. A title
2. An abstract. Make it clear you'll be printing the abstract!
3. A bulleted outline. If you don't ask for it in the CFP, you'll end up asking those who don't supply it anyway.
4. What attendees will gain.  This could be processes, tools, knowledge.  But it's the 2nd most common question I have to ask after asking for an outline.  It also helps distinguish between vendor pitches and useful talks.  Vendors will often speak about how _they_ did something but not necessarily how attendees can do it.
5. An attachment field.  This will let people share slides, longer outlines, detailed explanations of the talk, etc.  It's important for people who want to answer your specific questions but feel they have more they need to share.

The rating

Set your raters up for success.  You can ask your reviewers to answer lots of questions about talks, but the reality is only a few will be used.  I'd recommend 3 (stolen from bsidesNash:

1. Content (0-5). How good is the content and the speaker's likely ability to give it.
2. Applicability (0-5). How applicable is the content to the conference/track/interests of attendees/etc.
3. Comments/notes to submitters.

Most other questions will likely be another way of asking all or a portion of either question one or question 2.  For example, asking "Has this speaker done a good job in previous talks?" is really just a question to help predict the quality of the content.

1 and 2 could be combined into a single accept-reject range of 0-5.  I like the two as neither I nor other raters I've worked with have had trouble answering both questions for all talks.  Also, they are orthogonal with very little affect of one on the other.

I also recommend 0-5.  Honestly, it can be 0 to anything.  The goal is simply to have a range that normalizes to 0%-100% easily.  1-5 does not.  Is 1-5 20%, 40%, 60%, 80% and 100%?  is it 0%, 25%, 50%, 75%, 100%? It's unclear how it maps out. Terms are even worse. "really bad", "bad", "ok", "good", "really good"?  Is that 0/25%/50%/75%/100%? If so, just use those numbers.  0-5 is easily 0/20/40/60/80/100%.  You could also simply provide a slider from 0 to 1 to allow people to provide the granularity they want.

Every rater should leave some note that can be passed to the submitter.  They may be passed directly, summarized, or aggregated, but you'll need those notes.

Each rater will probably also keep their own notes that do not get shared with the submitter.  It's honestly never clear to raters which comment field will or won't be seen by the submitter in the online review system so you might as well have a single one that will be shared and tell raters to keep private comments offline.  It also helps the raters think about how to communicate their feedback positively.

I'd also recommend making raters provide a rating before seeing the submitter.  Even if they can go change their score after the fact, it helps remove implicit bias based on the submitter. It's ok if a rater rates something, sees the submitter and updates their opinion based on the additional information about the org, previous talks be the speaker, etc that they can clearly articulate.  But you don't want the information about the submitter, their company, experience, other submissions, etc influencing the rating implicitly and you don't want submitter ethnicity, gender, sexual orientation, etc influencing it at all.

Pre-rating

There are two things you should do as soon after CFP submission closes as possible, even before rating the talks.

1. Identify talks that should be moved to another track/reviewer.  
2. Identify talks where you need to ask the submitter a question to accurately review the talk.

These two things are impossible to accomplish late in the review process.  The first only really applies if you have multiple tracks with multiple raters.  But if you wait to move a submission, more than likely the receiving rater will already be done and won't be interested in another talk.  

For questions, it often only takes minutes, hours or a day to get an answer back, but if the review team is all on the phone making selections, that answer will be too late.  Even if it's to ask for an outline, a more detailed explanation of the submission, or what attendees can expect to learn, most submitters have an answer and can get it to you quickly.

Try to do a pass through the submissions before reviewing and identify any submissions that fall into either category.  Addressing it up front will lead to better outcomes for everyone at review time.

The review

After the ratings are in, it's time to review them to pick the talks:

1. Start with some mathematical analysis of your talks.  I do it with two scores in this blog, but it works just as easily with a single rating per talk.  Being able to visually check a talk's scores is strikingly helpful.  I've watched it save CFPs that were completely off track, take review meetings that were going no-where and turn them around, and half the time reviewing takes.
2. Start with the talks that everyone rated perfect or near perfect.  If everyone agreed they're good, don't waste time rehashing it.  Mark these "accept".
3. Then go to the bottom of the list and work your way up.  Basically, if no-one is willing to fall on their sword for the talk, "reject" it or mark it on the bubble.  (We tend to use "bubble up" or "bubble down".  Up for talks you'd accept if you could.  Down for talks you'd only take if you have to.)  
4. At some point you're going to get to talks that people liked, but had some flaw.  Raters will be saying "I liked this one, but..." That means you're now into the middle section of the talks.  Go back to the top, after the talks you've already accepted, and work your way down marking "accept", "reject", "bubble up", or "bubble down".  Be biased against accepting.  It's easier to go to the bubble to add talks than to accept more talks than you can take and cut again
5. Identify backup speakers.  How many is up to you, but I like 1 per track per day.  (Add at least one extra if international speakers are accepted as many things can prevent them from speaking.) I also like to identify someone on staff that will 'just be there' who can be easily found and give a talk (rather than having an empty room) if anything goes wrong.

Also, we tend to give reviewers one veto each; usually a talk they absolutely want, that they can use to overwrite the prevailing opinion of the group.

The notification

Now the part no CFP organizer likes, notifying people (particularly the non-acceptances).  This happens in a few stages:

1. Notify all of the accepts.  You need all of them to confirm that they can still make it.  Until they confirm, you don't have a talk.  That said, this normally happens pretty quickly.  Accepted people are exciting and generally respond fast.
2. Notify the bottom 3/4ths of the non-accepts.  You can't notify all because you may have some accepts that can no longer make it and so some of the non-accepts may turn into accepts.
3. Once you have all the accepts complete, notify the backups and get their confirmation. (Note that if some of your accepts didn't confirm, you may need to move a backup to an accept and a bubble-up to a backup.)
4. Finally notify any non-accepts that have not been notified.

All non-accepts deserve some feedback on why they weren't accepted.  It could be that the content wasn't the right fit, that the talk felt too complex or not complex enough.  it could be that the reviewers felt attendees wouldn't take a lot away from the talk.  It could be there were grammatical errors in the abstract.  It could simply be there wasn't enough information for raters to be confident it would be a good talk.  But all non-accepts deserve to hear from you.

And the rest of it

At this point, it turns into a speaker management job.  Making sure they have everything they need, know where to be and what to do.  That lasts until the speaker has completed their talk, but that's a subject for another post.

Data Driven Security Strategy

I presented on building a data driven security strategy at RSA this year.  You can find the video here and the slides here.

If there's one thing to take away it's this:

"Strategy is HOW YOU CHOOSE plans to meet your objectives, not the plans you choose. Those plans must be in the context of the rest of security and your organization. And a data driven security strategy is using MEASURES TO CHOOSE."

Data Analysis Template

This is just a quick blog to share my jupyter notebook analysis template.  I analyze a lot of different datasets in a short period, so having the analysis consistent is very helpful.  I'll walk through the sections quickly to share a bit about my process.

Title Section

In the title section, I have a block for any ideas to explore, specific things I intend to do, anything I need to request to be updated in the data, and any notes about the data.  These are all bulleted text boxes.

This section is VERY helpful for working on multiple datasets.  it's easy to forget what you were going to do or what you've done and the summary up front helps get you back in place.

Preparation

next is preparing the data.  No data comes ready for analysis.  Here I have blocks to read in the data, clean the created dataframe, save it to an R data (Rda) object on disk, and then, the next time I need it, I just load the Rda and skip the cleaning.

Analysis

The analysis section is basically filled with mini experiments.  each chuck is one.  As such, it's important that each have a bit of information in comments at the top of it:

1. A description of the hypothesis being tested or explored.  Something like "looking at the distribution of the periodicity of events".
2. Once it's done, describe the results.  Yes, the results should describe the results but you'll thank past you if you write down what you got from the analysis when you did it.  Something like "it looks like the periodicity is bimodal with one mode representing X and another representing Y."
3. Add a comment with a UUID.  Seriously.  Every. Single. Block.  If it's something interesting you're going to put it in a document or a blog or something.  You want to be able to track it from beginning to end.  (Ours track from the report, through several drafts of the report, through drafts of the sections, to a figures rmarkdown file that generates all the figures, to an exploratory report where we created the original analysis.)  Seriously.  If you like it then you shoulda put a UUID on it.
4. Now you can actually write the analysis code

Appendixes

This is where I put all of the extra stuff.

Testing

I always have a testing block.  Throughout the analysis, you'll spend a lot time testing stuff to make it work, (or simply looking up things like the dimensions of your data and the column names).  Putting those in a testing block keeps you from coming back later and wondering what the block in your analysis was there for.

Lookups

Sometimes you have big, ugly, lookups.  putting them at the top clogs the Preparation section, so I tend to put them at the bottom.  You'll remember you forgot to run them when your analysis fails.

Backup

Really a parking lot for anything you don't want in another section, but don't want to delete.

Ultimately, if I were doing full modeling, I'd probably want a template that follows the process outlined in Modern Dive.  However, for someone just getting into analysis, hopefully this helps!

Game Analysis of the 2018 Pros vs Joes CTF at BSidesLV

Introduction

Capture the Flag (CTF) contests are a staple of security conferences and BSides Las Vegas is no exception.  However the Pros vs Joes (PvJ) CTF I help support there is a bit unique.  Not only is it a blue vs blue CTF with red aggressor and gray user teams, but the game dynamics are a fundamental development point for the CTF team. (There's a lot more to it such as it's educational goal or that we allow blue teams to attack each other on the second day.  You can read more about it at http://prosversusjoes.net/.)

Game Dynamics

When we say 'game dynamics', we mean a couple of things.  First we mean what's scored and how much.  In our case that is currently four things:

• hosts (score given to teams for maintaining service availability)
• beacons (score deducted when the red team signals a host is compromised)
• flags (score deducted when the red team breaches specific files)
• tickets (score deducted when the gray team is not being appropriately supported)

At a more fundamental level though, we mean the scenario the CTF is meant to represent.  As a blue team CTF, we try and simulate the real world.  As such, starting last year, we began to transition our game model to simulate an economy.  Score is not granted so much as transferred.  For example, the gold team pays the gray team for accomplishing some task, then the gray team pays a portion of that score to the blue team for maintaining the services necessary to accomplish that task.  Alternately, when the red team (or another blue team) installs a beacon, the score isn't lost, but instead transferred to the team that placed the beacon.

Beginning with last year,  we have started to then simulate the way we expect the game to run.  This year we have also captured detailed scoring logs.  This blog is about our analysis of the score from this year's game and how it helps us plan for the future.

Simulation

The first thing we do is create a game narrative and scoring profile for the game.  The profile is the servers that will come online, go offline, and how much they will be scored per (5 minute) round.  It is picked to produce specific outcomes such as inflation (to decrease point value early in the game when teams are just getting going and to allow dynamism throughout the game).

We then try and build distributions of how likely servers will be to go offline, how likely beacons will be and how long they will last, and how many flags will be found.  This year we used previous years simulations and logs as well as expert opinion to build the distributions.   The distributions we used are below:

### Define distributions to sample from

## Based on previous games/simulations and expert opinion

# H&W outage distributions

doutage_count <- distr::Norm(mean=8, sd = 8/3)

doutage_length <- distr::Norm(mean=1, sd = 1/3)

# flag distributions

dflags <- distr::Norm(mean=2, sd= 2/3) # model 0 to 4 flags lost with an average of 2

# beacon distributions

gamma_shapes <- rriskDistributions::get.gamma.par(p=c(0.5, 0.7), c(0.75, 4)) # create a gamma distribution to draw number of tickets from

dbeacons_length <- distr::Gammad(shape=gamma_shapes['shape'], scale=1/gamma_shapes['rate']) # in hours

dbeacon_count <- distr::Norm((4-3)/2+3, (4-3)/3)

Based on this we ran Monte Carlo simulations to try and predict the outcome of the game.

First, we analyzed the expected overall score.

 Next we wanted to look at the components of the score.

Finally we wanted to look at the distributions of potential final scores and the contributions from the individual scoring types

The Game

And then we run the game.

The short answer is, it's VERY different.  We had technical issues that prevented starting the game on time.  We were not able to complete some development that prevented automatic platform deployment, some hosts were not available, and some user simulation was also not available. This is not a critique of the development team who did a crazy-awesome job both rebuilding the infrastructure for this game in the months leading up to it as well as dynamically deploying hosts during the game.  It's just reality.  The scoring profile was built for everything we want.  I am pleased with how much of it we got on game day.

The Scoreboard

The Final Scoreboard

You can find the final scoreboard and scores here.  It gives you an idea of what the game looked like at the end of the game, but doesn't tell you a lot about how we got there.  I'm personally more interested in the journey than the destination so that I can support improving the game narrative and scoring profile for the next game.

Scores Over Time

The first question is how did the scores progress over time?  (You'll have to forgive the timestamps as they are still in UTC I believe.)   What we hoped for was relatively slow scoring the first two hours of the game.  This allows teams the opportunity to make up ground later.  We also do not want teams to follow a smooth line or curve.  A smooth line or curve would mean very little was happening.  Sudden jumps up and down, peaks and valleys,  mean the game is dynamic.

What we see is a relatively slow beginning game.  This is due to beacons initially being scored below the scoring profile and one of three highly-scored puzzle servers being mistakenly scored lower from it's start late in day 1 until it was corrected at the beginning of day 2.

We do see an amount of trading back and forth.  ForkBomb (as an aside, I know they wanted the _actual_ fork bomb code for their name, but for this analysis text is easier) takes an early lead while Knights suffer some substantial losses (relative to the current score).  Day two scores take off.  The teams are relatively together through the first half of day 2, however, Arcanum takes off mid-day and doesn't look back.

The biggest difference is that when teams started to have several beacons, as part of their remediation they tended to suffer self-inflicted downtime.  This caused a compound loss of score (the loss of the host scoring they would have had plus the cost of the beacons).  We did not account for this duplication in our modeling, but plan to in the future.

Ultimately I take this to mean scoring worked as we wanted it to.  The game was competitive throughout and the teams that performed were rewarded for it.

It does leave the question of what contributed to the score...

Individual Score Contributions

What we expect is relatively linearly increasing host contributions with a bit of an uptick late in the game and linearly decreasing beacon contributions.  We also expect a few significant, discrete losses to flags.

What we find is roughly what we expected but not quite.  The rate of host contribution on day two is more profound than expected for both Paisley and Arcanum suggesting the second day services may have been scored slightly high.

Also, no flags were captured.  However, we do have tickets which were used by the gold team to incentivize the blue teams to meet the needs of the gray team.

The biggest difference is in beacons.  We see several interesting things.  First, for a period on day two, Knights employed a novel (if ultimately overruled) method for preventing beacons.  We see that in the level beacon score for an hour or two. We also see a shorter level score in beacons later on when the red team employed another novel (if ultimately overruled) method that was significant enough that had to be rolled back.  We also see how Arcanum benefited heavily from the day 2 rule allowing blue-on-blue aggression.  Their beacon contribution actually goes UP (meaning they were gaining more score from beacons than they were losing) for a while.  On the other side, Paisley suffers heavily from blue-on-blue aggression with significant beacon losses.

Ultimately this is good.  We want players _playing_, especially on day 2.  Next year we will try to better model the blue-on-blue action as well as find ways to incentivize flags and provided a more substantive and direct way for the gray team to motivate the blue team.

Before we move on, two final figures to look at.  The first lets us see individual scoring events per team and over time.  The second shows us the sum of beacon scores during each round.  It gives an idea of the rate of change of score due to beacons and provides an interesting comparison between teams.

But there's more to consider such as the contributions of individual hosts and Beacons to score.

Hosts

The first thing we want to look at is how the individual servers influenced the scores.  What we want to see is starting servers contributing relatively little by the late game, desktops contributing less, and puzzle servers contributing substantially once initiated.  This is ultimately what we do see.  (This was the analysis, done at the end of day 1, that allowed us to notice puzzle-3 scoring substantially lower than it should.  We can see it's uptick on day 2 as we correct it's scoring.)

It's also useful to look at the score of each server relative to the other teams.  Here it is much easier to notice the absence of the Drupal server (removed due to technical issues with it).  We also notice some odd scoring for puzzle servers 13 and 15, however the contributions are minimal.

More interesting are the differences in scoring for servers such as Redis, Gitlab, and Puzzle-1.  This suggests maybe these servers are harder to defend as they provided score differentiation.  Also, we notice teams strategically disabling their domain controller.  This suggests the domain controller should be worth more to disinsentivize this approach.

Finally, for the purpose of modeling, we'd like to understand downtime.  It looks like most servers are up 75% to near 100% of the time.  We can also look at the distributions per team.  We will use the distribution of these points to help inform our simulations for the next game we play.  We are actually lucky to have a range of distributions per team to use for modeling.

Beacons

For the purpose of this analysis, we consider a beacon new if it misses two scoring rounds (is not scored for 10 minutes).

First it's nice to look at the beacons over time.  (Note that beacons are restarted between day 1 and day 2 during analysis.  This doesn't affect scoring.)  I like this visualization as it really helps show both the volume and the length of beacons and how they varied by team.  You can also clearly see the breaks in beacons on day two that are discussed above.  

The beacon data is especially helpful for building distributions for future games.  First we want to know how many beacons each team had:

Day 1:

• Arcanum - 17
• ForkBomb - 24
• Knights - 18
• Paisley - 21

Day 2:

• Arcanum - 13
• ForkBomb - 17
• Knights - 29
• Paisley - 34

We also want to know how long the beacons last. The aggregate distribution isn't particular useful. However the distributions broken out by teams are interesting.  They show substantial differences between teams.  Arcanum had few beacons, but they lasted a long time.  Paisley had very few long beacons (possibly due to self-inflicted downtime).  Rather than be a power law distribution, the beacons are actually relatively even with specific peaks.  (This is very different from what we simulated.)

Conclusion

In conclusion, the take-away is certainly not how any given team did.  As the movie "Any Given Sunday" implied, sometimes you win, sometimes you lose.  What is truly interesting is both our ability to attempt to predict how the game will go as well as our ability to then review afterwards what actually happened in the game.

Hopefully if this blog communicates anything, it's that the scoreboard at the end simply doesn't tell the whole story and that there's still a lot to learn!

Future Work

This blog is about scoring from the 2018 BSides Las Vegas PvJ CTF so doesn't go into much detail about the game itself.  There's a lot to learn on the PvJ website.  we are also in the process of streamlining the game while making the game more dynamic.  As mentioned above, the process started in 2017 and will continue for at least another year or two.  Last year we added a store so teams can spend their score.  We also started treating score as a currency rather than a counter.

This year we added additional servers coming on and off line at various times as well as began the process of updating the gray team's role by allowing them to play a puzzle challenge hosted on the blue team servers.

In the next few years we will refine score flow, update the gray team's ability to seek compensation from the gray team for poor performance, and additional methods to maximize blue team's flexibility in play while minimizing their requirements.  Look forward to future posts as we get the details ironed out!